Unityと数学と音楽の学習帳

Unityと数学、音楽の同時学習を目的としたブログ（個人的メモ帳：勉強中なので正確性はない）

最小二乗法の学習忘備録

PocketCas 最小二乗法 数学 統計

該当記事のディテールを補足する個人的な忘備録

以下のサイトを参考に最小二乗法の仕組みを学習する
qiita.com

基本戦略

「基本戦略」の部分をグーグルスプレッドシートで確認したものが以下になる

docs.google.com

最小化する

「極大極小の考え方でいうと、a, bそれぞれに対して、微分して0になるところが最小点になります。」の語句の意味をIOSアプリのPocketCasを利用して再確認すると以下になる

例えば二次関数の微分に対して０になる方程式を解くと以下の様に最小点のx=1.5が算出できる
f:id:cqbosinko:20170713003931p:plain

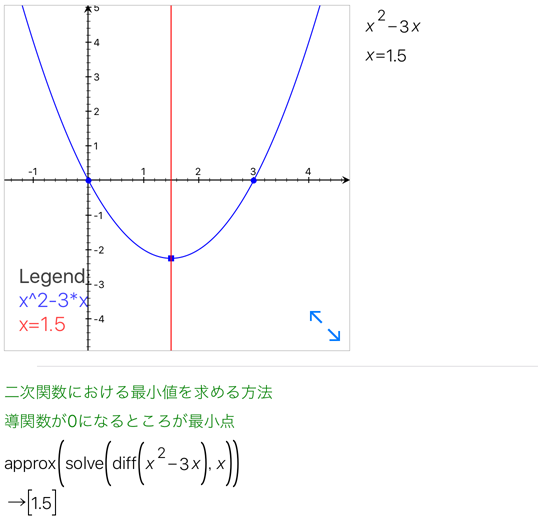
これは他のn次数関数に対しても同様で三次関数の場合、グラフの谷山になるx位置
x=-3.0とx=-1/3が算出できる。つまりグラフの傾きが0になる位置がわかる仕組みを利用する
f:id:cqbosinko:20170713004657p:plain

5次関数で以下のようになる。微分の強力な解析能力が実感できる
f:id:cqbosinko:20170713004901p:plain

この解析能力をaとbの二変数関数である{ \left( y_{ i }-a{ x }_{ i }-b \right) }^{ 2 }に対して利用する為に偏微分しようという訳である。偏微分はaとbに対して行い他の変数は定数と扱われる。導かれた導関数が０になる連立方程式を解くと最小点の位置を通る一次関数の係数が解るという仕組みになる

実際の計算

あてはめる関数式は直線をあらわす一次関数。これを回帰式と呼ぶ

f\left( x \right) =ax+b

回帰式と実際に集計した値との誤差を求める式が以下になる
y値、x値はN次のベクトル。これらを総和を利用しながら誤差の総和Jの値を導く
aとbは未知数でJの値を最小にしながら、これらの値を求める事が目的となる

J\quad =\quad \frac { 1 }{ 2 } \sum _{ i=1 }^{ N }{ { \left\{ y_{ i }-\left( a{ x }_{ i }+b \right) \right\} }^{ 2 } } \quad =\quad \frac { 1 }{ 2 } \sum _{ i=1 }^{ N }{ { \left( y_{ i }-a{ x }_{ i }-b \right) }^{ 2 } }

シグマの中身は常に二乗されるので値は絶対値、距離、正数となる
従って、この二次関数の微分された関数式は0になる所が最小点に必ずなる（最大値になる可能性は無い。だからこの計算手法は「最小二乗法」と呼ばれる）
関数式の中にaとbの二変数の未知数があるので、それぞれ偏微分して０になる式を導き連立方程式を組む必要がある
偏微分には例題となるブログでは合成関数「\left\{ g\left( f\left( x \right) \right) \right\} '=g'\left( f\left( x \right) \right) \cdot f'\left( x \right)」を利用している

\frac { \partial J }{ \partial a } \quad =\quad \frac { 1 }{ 2 } \sum _{ i=1 }^{ N }{ 2{ \left( y_{ i }-a{ x }_{ i }-b \right) } } \left( { -x }_{ i } \right) \quad =\quad a\sum _{ i=1 }^{ N }{ { x }_{ i }^{ 2 } } +b\sum _{ i=1 }^{ N }{ { x }_{ i } } -\sum _{ i=1 }^{ N }{ { x }_{ i }y_{ i } } \\ \frac { \partial J }{ \partial b } \quad =\quad \frac { 1 }{ 2 } \sum _{ i=1 }^{ N }{ 2{ \left( y_{ i }-a{ x }_{ i }-b \right) } } \left( -1 \right) \quad =\quad a\sum _{ i=1 }^{ N }{ { x }_{ i } } +b\sum _{ i=1 }^{ N }{ 1 } -\sum _{ i=1 }^{ N }{ y_{ i } }

最終的な回帰式は行列計算の形になる
これは連立方程式を計算機で解く為で、機械を使って問題を解く適切な形となっている

\begin{cases} a\sum _{ i=1 }^{ N }{ { x }_{ i }^{ 2 } } +b\sum _{ i=1 }^{ N }{ { x }_{ i } } -\sum _{ i=1 }^{ N }{ { x }_{ i }y_{ i } } =0\quad \Leftrightarrow \quad a\sum _{ i=1 }^{ N }{ { x }_{ i }^{ 2 } } +b\sum _{ i=1 }^{ N }{ { x }_{ i } } =\sum _{ i=1 }^{ N }{ { x }_{ i }y_{ i } } \\ a\sum _{ i=1 }^{ N }{ { x }_{ i } } +b\sum _{ i=1 }^{ N }{ 1 } -\sum _{ i=1 }^{ N }{ y_{ i } } =0\quad \Leftrightarrow \quad a\sum _{ i=1 }^{ N }{ { x }_{ i } } +b\sum _{ i=1 }^{ N }{ 1 } =\sum _{ i=1 }^{ N }{ y_{ i } } \end{cases}\\ \\ \begin{pmatrix} \sum _{ i=1 }^{ N }{ { x }_{ i }^{ 2 } } & \sum _{ i=1 }^{ N }{ { x }_{ i } } \\ \sum _{ i=1 }^{ N }{ { x }_{ i } } & \sum _{ i=1 }^{ N }{ 1 } \end{pmatrix}\begin{pmatrix} a \\ b \end{pmatrix}=\begin{pmatrix} \sum _{ i=1 }^{ N }{ { x }_{ i }y_{ i } } \\ \sum _{ i=1 }^{ N }{ y_{ i } } \end{pmatrix}\quad \quad \Leftrightarrow \quad \begin{pmatrix} a \\ b \end{pmatrix}={ \begin{pmatrix} \sum _{ i=1 }^{ N }{ { x }_{ i }^{ 2 } } & \sum _{ i=1 }^{ N }{ { x }_{ i } } \\ \sum _{ i=1 }^{ N }{ { x }_{ i } } & \sum _{ i=1 }^{ N }{ 1 } \end{pmatrix} }^{ -1 }\begin{pmatrix} \sum _{ i=1 }^{ N }{ { x }_{ i }y_{ i } } \\ \sum _{ i=1 }^{ N }{ y_{ i } } \end{pmatrix}

この行列式に実測値をあてはめ計算していく

{ x }_{ i }=\left\{ 4,15,30,50 \right\} \\ y_{ i }=\left\{ -17,-4,-7,25 \right\}

a\sum _{ i=1 }^{ N }{ { x }_{ i }^{ 2 } } \quad =\quad a\left( { 4 }^{ 2 }+{ 15 }^{ 2 }+30^{ 2 }+{ 50 }^{ 2 } \right) \quad =\quad 3641a\\ b\sum _{ i=1 }^{ N }{ { x }_{ i } } \quad =\quad b\left( 4+15+30+50 \right) \quad =\quad 99b\\ \sum _{ i=1 }^{ N }{ { x }_{ i }y_{ i } } \quad =\quad 4\times -17+15\times -4+30\times -7+50\times 25\quad =\quad 912\\ a\sum _{ i=1 }^{ N }{ { x }_{ i } } \quad =\quad a\left( 4+15+30+50 \right) \quad =\quad 99a\\ b\sum _{ i=1 }^{ N }{ 1 } \quad =\quad 4b\\ \sum _{ i=1 }^{ N }{ y_{ i } } \quad =\quad -17+-4+-7+25\quad =\quad -3

\begin{pmatrix} a \\ b \end{pmatrix}={ \begin{pmatrix} 3641 & 99 \\ 99 & 4 \end{pmatrix} }^{ -1 }\begin{pmatrix} 912 \\ -3 \end{pmatrix}

pocketcasで計算させると以下になる

f:id:cqbosinko:20170716135453p:plain

数について

数学 数理

どんな数も合成数である
数には人間に理解の及ぶ範疇と及ばない範疇があり、それは例えば前者の場合、自然数や有理数、後者の場合、無理数や虚数等となってイメージされる
それらを大雑把にふたつにわけ、「良い数」「悪い数」と考えることもできる

良い数をu、悪い数をvと考え、数そのものを「u+v」という合成数で考えることもできる
たとえば以下のような式がある

x=1+\frac { 1 }{ x }

両辺にxがあるので解（根）は求まっていない。とりあえず両辺にxがある状態を無くす必要がある。なので、これを変形していく。すると解は黄金数になる。変形にはややアクロバティックな正方完成の考えが利用される

\Leftrightarrow \quad x\cdot x=1\cdot x+\frac { 1 }{ x } \cdot x\quad \Leftrightarrow \quad { x }^{ 2 }=x+1\\ \Leftrightarrow \quad { \left( x-\frac { 1 }{ 2 } \right) }^{ 2 }+x-\frac { 1 }{ 4 } =x+1\quad \Leftrightarrow \quad { \left( x-\frac { 1 }{ 2 } \right) }^{ 2 }=x+1-x+\frac { 1 }{ 4 } \quad \Leftrightarrow \quad { \left( x-\frac { 1 }{ 2 } \right) }^{ 2 }=\frac { 5 }{ 4 } \\ \Leftrightarrow \quad x-\frac { 1 }{ 2 } =\pm \sqrt { \frac { 5 }{ 4 } } \quad \Leftrightarrow \quad x-\frac { 1 }{ 2 } =\frac { \pm \sqrt { 5 } }{ 2 } \quad \Leftrightarrow \quad x=\frac { 1\pm \sqrt { 5 } }{ 2 }

この場合、1がよい数で\sqrt { 5 } が悪い数になる。こういう合成数の図式はあらゆる場面で見られる。たとえば複素数もそうであるし、サインコサインの出力値、漸化式の解や別の形に表現された無理数もよく見ると、この形になっていたりする（０は良い数、悪い数、両方の性質を持つと考える）
そういったセンスを持っておくと色々得をしそう？（テイラー展開でとか？？）

循環小数の作成

数学 数理 確率

参考資料：
www.4gamer.net

0.3939393939...\quad =\quad 0.\dot { 3 } \dot { 9 } 　のような循環小数の作成

基本的に以下の様な仕組みを利用する。これはゲーム開発では乱数の作成の基礎などに利用できる

\lim _{ n\rightarrow \infty }{ { S }_{ n } } \quad =\quad 39\left\{ \frac { 1 }{ 100 } +{ \left( \frac { 1 }{ 100 } \right) }^{ 2 }+{ \left( \frac { 1 }{ 100 } \right) }^{ 3 }+\cdots +{ \left( \frac { 1 }{ 100 } \right) }^{ n } \right\}

等比数列の和の公式 { S }_{ n }=\frac { { a }_{ 1 }\left( 1-{ r }^{ n } \right) }{ 1-r } を利用して

\lim _{ n\rightarrow \infty }{ { S }_{ n } } =39\times \frac { \frac { 1 }{ 100 } \left( 1-{ \left( \frac { 1 }{ 100 } \right) }^{ n } \right) }{ 1-\frac { 1 }{ 100 } } \\ { S }_{ n }=\quad 39\times \frac { \frac { 1 }{ 100 } \left( 1-0 \right) }{ 1-\frac { 1 }{ 100 } } \quad =\quad 39\times \frac { \frac { 1 }{ 100 } }{ \frac { 99 }{ 100 } } \quad =\quad 39\times \frac { 1 }{ 99 } \quad =\quad \frac { 13 }{ 33 }

となる。簡単に言うと39÷99で循環小数を作れるし、例えば0.1234512345...のような場合は、12345÷99999で作れる。乱数にしたいなら、この99の部分を98や97にずらしていく。（もちろんこんなものは乱数ではないのだが、ぱっとみて乱数と勘違させることは出来る）この循環少数の狙った桁や並んだ数字部分を抽出したいのなら以下のような考え方を利用する（10なら一桁づつだが100にすればふたつずつ抽出するなども出来る）


狙った桁の抽出

線形計画問題、忘備録

PocketCas 数学

資料：
線形計画問題
f:id:cqbosinko:20170501195822p:plain

このようなグラフを書くことによって、どんな情報が得られるかに注目した方が良い。このグラフから、この問題をうまく解決すれば最低でも6000円以上、10000円以下の利益が得られることが分かる。また、理屈で考えるとx=800,y=8が最適解となる事が考えられる（図を書かなければそんなことはイメージ出来ない）

また図を描く事とは別として行列の計算、アルゴリズムを利用して線形代数的に最適解を算出することが可能となる

unityチュートリアル　「2D UFO」のメモ

unity
  • テクスチャ画像をシーンにドラッグすると勝手にスプライトレンダーコンポーネントが付加される
  • ソーティングレイヤーは描画順
  • コライダーコンポーネントはひとつのゲームオブジェクトに複数作り組み合わせることができる
  • プレハブは青く表示される。ヒエラルキーからプロジェクトにドラッグすると自動的に作れる
  • ctrl+cとctrl+vでもコピーできるが、ctrl+dでも出来る
  • コライダーの設定で「Is Trigger」をオンにすると物理的な跳ね返りがなくなる（通り抜けてトリガーが発行される）
  • RigedBody2DのBodyTypeを「Kinematic」にするとunity内の物理作用はゼロになり、トランスフォームのみで動くようになる

　これにより処理が軽くなる

  • 以前のバージョンと違ってunityのUIは名前空間 unityengine.UIで拡張されている

　仕様がまるで変っている。textひとつとっても扱い方が変わっているので再学習の必要アリ


UI関連

  • 今までと違いCanvas内のオブジェクトに対してはショートカットtで色々なトランスフォームとは別の操作が可能となる

（posやwidth、heightなど）

  • RectTransformを持つオブジェクトの場合ヒエラルキーウインドウ内で選択した状態で右クリック->CreateEmptyすると

　空のUIの子が簡単に作れる

  • レンダーテクスチャはCreate -> RenderTexture　で作成できる。これをカメラに設定すると良い
                                                                                                                                                                                        • -


＜カメラ操作tips＞
カメラオブジェクトを選択した状態で　ctrl+Shift+f で　カメラをビューの視点に出来る
ビューはビュー内のどこかをクリックして選択状態にするとカーソルキーが使えるようになる

ゲーム性を向上させる確率の考え方

確率 数学 数理

指数と確率の考え方

>20%の5連撃を1発でも当てれば…なんて時にサクーッと概算できるようになっても
>2の10乗が1000って覚えとくと便利よね

{ 2 }^{ 10 }\quad =\quad 1,024\quad \simeq \quad { 10 }^{ 3 }\\ { 2 }^{ 20 }\quad =\quad 1,048,576\quad \simeq \quad { 10 }^{ 6 }\\ { 2 }^{ 30 }\quad =\quad 1,073,741,824\quad \simeq \quad { 10 }^{ 9 }


>全部外れる確率は
>0.8の5乗 → 2の15乗の上一桁の数字だけほしい → 3
>だから7割くらいは1発当たるはず

0.8^{ 5 }\quad =\quad (0.1\times 8)^{ 5 }\quad =\quad 0.1^{ 5 }\times (2^{ 3 })^{ 5 }\quad =\quad 0.1^{ 5 }\times 2^{ 15 }\quad =\quad 0.32768

この７割ってのは必ず５回連続攻撃して、その内7割の確率でヒットするという考え方
つまり20%、40%、80%、と言う確率は計算しやすい。又、5回攻撃前提でワンパック（大数の法則）になっている点も強く意識しておく事が大事
ワンボタンで一度に５回攻撃が出るRPGの戦闘みたいな場面を想像すると良い

f:id:cqbosinko:20170414134223p:plain

＜メモ＞
桁と小数点位置の感覚がつかめていないと痛い目にあうので注意

指数関数はネイピア数を利用した指数関数と同相になる。対数関数とは逆関数の関係となる
（このグラフで考えると横軸に対する拡大縮小率で何回試行すれば充分かという考え方ができる筈。つまりネイピア数に対する係数がある筈）

第一回年末ジャンボと第二回年末ジャンボは写像が変わるので同相でなく不連続となる？
この場合、第一回と第二回を一緒にした写像を作れば連続となるが解は変わるか？

一桁のパーセンテージというのは、ほぼ大数の法則に支配されると考える。場の親であるなら
結果を安定させるために試行の単価（ランニングコスト）を安くして試行回数を増やす必要があると予想できる

「同相」という考え方は重要で強力
https://kotobank.jp/word/%E5%90%8C%E7%9B%B8-1189069
http://rikei-index.blue.coocan.jp/syugou/dousousya.html