指数と直感の話 - Unityと数学と音楽の学習帳

先日、郵便物を読んでいて興味深い数学の話があったので自分なりに記事を再検証してみることにした。
記事の内容をそのまま、ここに載せるのはリテラシーの面で問題があるので多少、問題の形を変えて考えてみる。

資料：瀬山士郎先生の数学よもやま話：連載15 ちょっとおかしな賭け
こんな賭けがある。100枚のカードがあり各カードには「WIN（勝ち）」、「LOSE（負け）」と書かれている。この100枚のカード全てを裏にして並べて置き、任意のカードを表にして「WINが出たら」現在の所持金の半分がもらえる。「LOSEが出たら」現在の所持金の半分が奪われる。このゲームを100枚のカード全部、表にするまで行う。とする。「WIN（勝ち）」のカードが61枚、「LOSE（負け）」のカードが39枚だとする。あなたは、この賭けにのりますか？

直観的に考えると、お金の出入りは半額同士なのでカードの配分を考えると自分が圧倒的に有利だと思う。
しかし、この賭けは罠だ。このゲームにのったら最期、自分の最終所持金が必ずほぼ10％になってしまう。

計算してみよう。

連続で61回勝利し、その後、連続で39回負けるとする。最初の所持金は100円とすると、式はこうなる

${ a }_{ 1 }=100\quad ,\quad { a }_{ n+1 }={ a }_{ n }+\frac { { a }_{ n } }{ 2 } \quad \left( n=1,2,3,\cdots ,60,61 \right) \\ \Rightarrow \quad { a }_{ n+1 }={ a }_{ n }\cdot \left( 1+\frac { 1 }{ 2 } \right) \quad \Rightarrow \quad { a }_{ n+1 }={ a }_{ n }\cdot \frac { 3 }{ 2 }$

漸化式と一般解の公式 ${ a }_{ n+1 }={ a }_{ n }r\quad \Rightarrow \quad { a }_{ n }={ a }_{ 1 }{ r }^{ n-1 }$ を利用して漸化式を一般式に変換すると

${ a }_{ 1 }=100\quad ,\quad { a }_{ n+1 }={ a }_{ n }\cdot \frac { 3 }{ 2 } \quad \left( n=1,2,3,\cdots ,60,61 \right) \quad \Rightarrow \quad { a }_{ 61 }=100{ \cdot \left( \frac { 3 }{ 2 } \right) }^{ 61+1-1 }$

これで61枚目を開いた状態の所持金の値になっているので、このまま続けて

$b_{ 1 }={ a }_{ 61 }\quad ,\quad b_{ n+1 }=b_{ n }-\frac { b_{ n } }{ 2 } \quad \left( n=1,2,3,\cdots ,38,39 \right) \\ \Rightarrow \quad { b }_{ n+1 }=b_{ n }\cdot \left( 1-\frac { 1 }{ 2 } \right) \quad \Rightarrow \quad b_{ n+1 }={ b }_{ n }\cdot \frac { 1 }{ 2 } \quad \Rightarrow \quad b_{ 39 }={ a }_{ 61 }{ \cdot \left( \frac { 1 }{ 2 } \right) }^{ 39+1-1 }$

従って100枚すべてめくった時の所持金は

$100{ \left( \frac { 3 }{ 2 } \right) }^{ 61 }{ \left( \frac { 1 }{ 2 } \right) }^{ 39 }$

となる。

この計算は乗算で閉じている。つまり演算項の順番、言い換えると勝ち負けの順番が自由に入れ替わっても100枚全部表にする以上、計算結果は変わらない事に注目する必要がある。
つまりどんなことをしようが、必ずこうなる。

$100{ \left( \frac { 3 }{ 2 } \right) }^{ 61 }{ \left( \frac { 1 }{ 2 } \right) }^{ 39 }=10.03221824771$

100円あった所持金は必ず10円になる。こういうペテンがあるのだ。
試行中の所持金の値をスプレッドシートで確認できるようにした。値が信じられないなら以下を参照

docs.google.com

さらにunity上でこのカードゲームをシミュレーションして結果を確認して置く

シャッフルしたカードのシミュレーション

3回のシミュレーション結果
CARD:WWWWLLWWWLWLLLLWLWWWLWWWWWWWLWWLLLLWWWWLWWWLWLWLLWWWLLLLWWWLLWLWLWWWWLWWWLWWWWWWWLLLLWLWWLLLWWWLLWWW money=10.03222
CARD:LWWLWWLWWWLWLWWWWWLWWWLLLWWWWWLWWLLLLLLWWWLLWLLWLWWWWLWWLWWLWLWWWLWLWLWWWWWLWWWLLWWWLLLLWWWWWWLLWLWL money=10.03222
CARD:WLWLWLWWLWWWWWLWWWLLWLWWWWLLLLLLWWLWLLLLLWWWLWWWLLWWLLWLLWWWLWLWLWWWWWWWWWWWWWLWWLWWLWWWLLWWWLWLWWLL money=10.03222

計算式は以下のようにpocketCasでも仕組みを検証できる

f:id:cqbosinko:20180830165345p:plain

この一連の問題は物事を指数に変換してみると分かりやすいと言う事を非常にシンプルに表している様な気がする、つまり...
$\frac { 1 }{ 2 } ,\frac { 2 }{ 2 } ,\frac { 3 }{ 2 }$ この３つの数字を2の指数表示にしてみると ${ 2 }^{ -1 },{ 2 }^{ 0 },{ 2 }^{ 0.5849625... }$
となる。-1と0.5849625...では値的にどちらが強いか？という風に考える事も出来る。要約すると以下のように考えるとさらにシンプルになる

${ \left( \frac { 3 }{ 2 } \right) }^{ 61 }{ \left( \frac { 1 }{ 2 } \right) }^{ 39 }\quad \Rightarrow \quad { \left( { 2 }^{ 0.5849625... } \right) }^{ 61 }{ \left( { 2 }^{ -1 } \right) }^{ 39 }\quad \Rightarrow \quad \left( { 2 }^{ 0.5849625...\times 61 } \right) \left( { 2 }^{ -1\times 39 } \right) \quad \quad \Rightarrow \quad \left( { 2 }^{ 35.68271... } \right) \left( { 2 }^{ -39 } \right)$

この右端の式は、勝敗のカードの枚数の配分が何枚なら、この賭けに乗ってもいいかの意味を単純に表している。
つまりWINのカードの枚数が、3.32乗分だけ、もう少し必要だと考えられる。
これはデシベルの考えに通じている。ここで同じ種類の2つの量の比として定義される量は無次元量である事を利用してみる。

参考資料：

2つの対数の量の比は底の値を変えても同じになる。これが物理量のレベル表現となる。関係をpocketCasの計算式で確認すると以下になる

f:id:cqbosinko:20181109104241p:plain

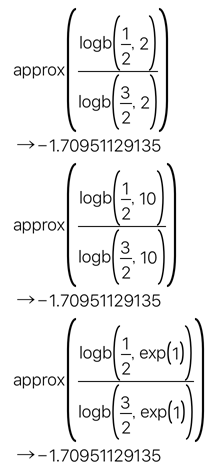
もう、底はなんでもいいという事なので、下の様な式を作って方程式を解くと、かならず勝てるラインが解ってくる

$\frac { 1.7095\times \left( 100-n \right) }{ n } =1\quad \Rightarrow \quad 170.95-1.7095n=n\quad \Rightarrow \quad 170.95=2.7095n\quad \Rightarrow \quad n=63.0928$

まとめるとWINのカードが64枚以上、必要だと言う事になる。

f:id:cqbosinko:20181109172342p:plain

よくTVゲームで強さをレベルで表現しているが、この仕組みを利用しているのではないだろうかと最近考えている。