ネイピア数の成り立ちを想像する - Unityと数学と音楽の学習帳

資料：虚数の情緒P515～P556
最初に指数関数を考える

$f\left( x \right) ={ a }^{ x }$

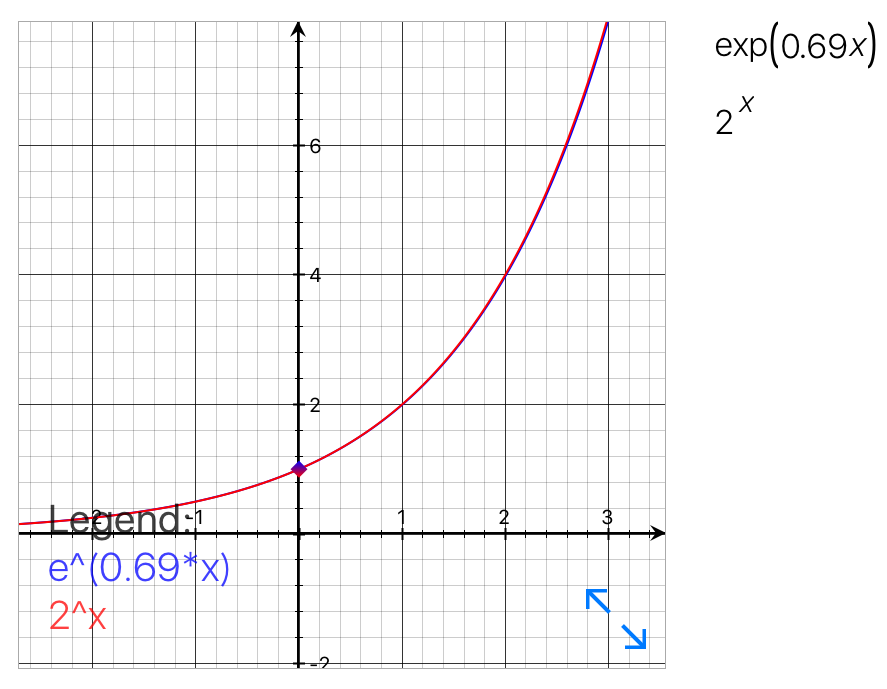
まず、自明な事として、あらゆる指数関数は $x=0$ の時、必ず、 $f\left( 0 \right) ={ a }^{ 0 }=1$ 　の点を通る。従って極小の $x$ 、例えば $x=0.000001$ において、様々な底を持つ指数関数の傾きの違いを観察すると、その性質や特徴が掴めるのではないか？と昔の数学者は考えたのかもしれない。極小の世界では曲線のグラフもほぼ直線のグラフの様に見える

f:id:cqbosinko:20190305204846p:plain

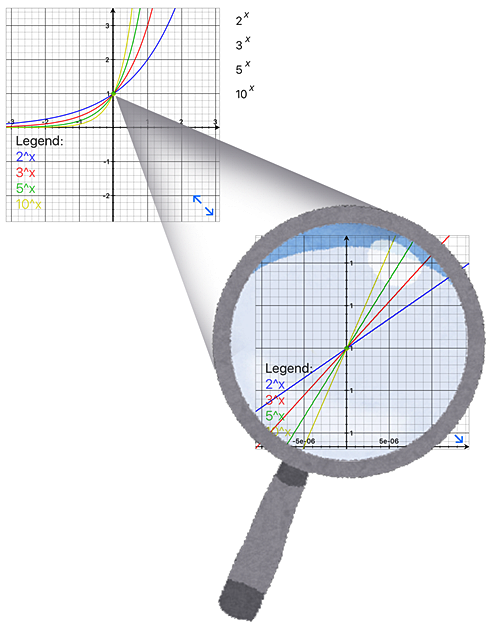
では実際に、入力値 $x$ に極小の値、 $x=0.000001$ を代入して関数電卓で指数関数の出力値を確認する

${ 2 }^{ 0.000001 }=1.000000693...\\ 3^{ 0.000001 }=1.000001099...\\ 5^{ 0.000001 }=1.000001609...\\ 10^{ 0.000001 }=1.000002303...$

計算結果は思った通り１周辺の小数点５桁目から違いが確認できるような値となっている
傾きを調べる為には $x=0$ と引いて差分を求める必要がある。つまり

$\displaystyle 傾き=\frac { 指数関数の極小の差分 }{ 入力値の極小の差分 } \quad \Rightarrow \quad f'\left( x \right) \simeq \frac { f\left( 0.000001 \right) -f\left( 0 \right) }{ 0.000001-0 }$

$x$ は極限まで小さい値とは言えないが、かなり小さい値である。この式を求めれば各底の指数関数の傾きが求められる

$\displaystyle \frac { { 2 }^{ 0.000001 }-{ 2 }^{ 0 } }{ 0.000001-0 } =\frac { 1.000000693...-1 }{ 0.000001 } =0.69314742...\quad \cdots ①\\ \displaystyle\frac { { 3 }^{ 0.000001 }-{ 3 }^{ 0 } }{ 0.000001-0 } =\frac { 1.000001099...-1 }{ 0.000001 } =1.09861289...\\ \displaystyle\frac { 5^{ 0.000001 }-5^{ 0 } }{ 0.000001-0 } =\frac { 1.000001609...-1 }{ 0.000001 } =1.6094392...\\ \displaystyle\frac { 10^{ 0.000001 }-{ 10 }^{ 0 } }{ 0.000001-0 } =\frac { 1.000002303...-1 }{ 0.000001 } =2.30258774...$

これが極小の世界の指数関数の傾きの違いだ。①を例にとって考える。これは $x$ が1進む間に $f\left( x \right)$ が0.69314742...進むという事を表している（数値の後ろの...はこの後ろに何桁も値が続いているが書ききれないので省略しているよ、と言う事を表している）。では反対に $f\left( x \right)$ が1進むと $x$ はどれだけ進むのだろうか？これは単純に $\frac { 1 }{ 0.69314742... }$ で求められる。では、この値を元の底に指数関数の入力として与えると何が求まるだろうか？これは「極小の傾き1の指数関数の底の値」を求めることになる。この計算には対数を利用するとよい。計算は以下になる。

$\displaystyle 極小の傾き1の指数関数の底の値\quad \simeq \quad \log _{ 2 }{ x } =\frac { 1 }{ 0.69314742... } \quad \Leftrightarrow \quad x={ 2 }^{ \frac { 1 }{ 0.69314742... } }=2.718280889...\quad \simeq \quad e$

ネイピア数は周知のとおり、 $e=2.718281828...$ 。その近似値を極小の世界に注目する事で簡単に求められる事がこれで確認できた。これは他の底を持つ指数関数でも同様に行える。

$\log _{ 3 }{ x } =\frac { 1 }{ 1.09861289... } \quad \Leftrightarrow \quad x={ 3 }^{ \frac { 1 }{ 1.09861289... } }=2.718280341...\quad \simeq \quad e\\ \log _{ 5 }{ x } =\frac { 1 }{ 1.6094392... } \quad \Leftrightarrow \quad x={ 5 }^{ \frac { 1 }{ 1.6094392... } }=2.718279654...\quad \simeq \quad e\\ \log _{ 10 }{ x } =\frac { 1 }{ 2.30258774... } \quad \Leftrightarrow \quad x=10^{ \frac { 1 }{ 2.30258774... } }=2.718278704...\quad \simeq \quad e$

ここで、「指数関数の極限を利用した傾き」の意味を振り返って考えてみると、指数関数の出発点、 $x=0,y=1$ の時点の"各底の勢い"（傾き）みたいなものだと考える事が出来る。
そこで、この"勢い"の違いを利用しようと考えると

$\log _{ e }{ x } =\frac { 0.69314742... }{ 1 } \quad \Leftrightarrow \quad { e }^{ 0.69314742... }\simeq 2$

この右辺の式は表現が違うだけで同じ値である事を表しているから、これを「底にして指数関数を作る」と

$\Rightarrow \quad { \left( { e }^{ 0.69314742... } \right) }^{ x }\quad \simeq \quad { \left( { 2 }^{ 1 } \right) }^{ x }\quad \Rightarrow \quad { e }^{ 0.693x }\quad \simeq \quad { 2 }^{ x }$

と考える事が出来る。関数の出発点の勢いをこれで同期させることになる。関数の表現は違うが出力は同じ値になる。
ここまで考えるとネイピア数が指数関数にとって数字の１のような基本になる定数値である事が理解しやすいと思う。
だから「自然対数の底（Base）」という名前が付けられていると考えられる。指数関数の極小の世界は不思議だ。
極小の世界の特徴、性質を掴む事で極大の性質、無限大に近い性質も掴む事が出来る。これが微分の意義と感じることも多い。

f:id:cqbosinko:20190305220619p:plain