某ゲームの確率計算、答え合わせ用プログラム
某ゲーム(NKODICE)の確率計算、答え合わせ用プログラムです。
順列、組み合わせ、重複などの樹形図の作成、数え上げを行います。
シンプルな構造なので確率計算などの答え合わせなどに応用が利くと思います。
TreeGenは変数lengthとsetの内容に従った順列を帰納関数の仕組みを使って生成し
樹形図が書かれたテキストファイル「Gen1.txt」を出力します。
(尚、帰納関数を利用しているので標本空間の要素数やダイスの施行回数が変わっても平気で動きます。これをうまく利用してください)
Reserchはテキストファイル「Gen1.txt」を読み込んでSerch関数内で作成した条件に合う集合を
数え上げ結果をテキストファイル「Result1.txt」で出力します。
出力先はunity内の生成される実行ファイルがある場所です。
(したがって通常unityのUI内のコンテンツフォルダ内を見れば実行後、生成されている筈です)
これをVisualStudioなどで閲覧すると便利です。
具体的にはunityを立ち上げ適当な名前でプロジェクトを作りシーン内に「Ctrl+shift+n」でGameObjectを作成。
これにコンポーネントに「クラスネームを合わせたスクリプト」を作成。これらにコピペして利用すれば良いです。
Reserchは「既存のGen1.txt」を読み込むのでTreeGenが先に動くようにしてください。
(面倒なら2回unityを「▷再生」すれば良いと思います)
giste0599dec2b6a9c008d7be651f7be915f
CakeWalk忘備録(長さ、グリッド)
cakewalkにおける音の長さ
四分音符=工場出荷状態で960ティック(CakeWalk独自の内部クロック数みたいなもの)
(他人が作ったプロジェクトの場合、このティック数が960以外の値になっている場合がある。デュレーションの値がヘンだと感じたら環境設定をチェックする事)
タイムは「小節:拍:ティック」で表示されている
デュレーション入力時「x:y」x=1が四分音符、y=960で四分音符
例:
「1:480」=付点四分音符
「240」=16分音符
「120」=32分音符
cakewalkにおけるグリッドについて

トラックビュー(プロジェクト内全体)とピアノロールビュー内、それぞれにグリッド設定があり
効果は、このふたつが同時に掛かる点に注意。フォーカスが点灯している状態がオンで
絶対スナップはタイムライン上に絶対値としてスナップ
相対スナップは現在配置されているノートの位置を基準に相対的にスナップ配置できる。
オプションとしてピアノロールビューでは
- MIDIイベントに対してスナップ
- マーカーに対してスナップ
それぞれ重複してオンに出来る
トラックビューのスナップ機能が親でピアノロールビューのスナップが子になっている
従って親のトラックビューのスナップ機能をオフにすると子もオフになる
逆に子であるピアノロールビューのスナップをオフにした場合、トラックビューのスナップ機能が生きてくる。
一般的にグリッド幅を「トラックビュースナップ>ピアノロールビュースナップ」にしておけば便利に使える場面が多い。
ピアノロールでのノートの描画
ctrl+altドラッグで現在のティックでノートを連続描画出来る
これに加えshiftを押しながらで直線に(3つのキーを押しながらドラッグ)
ノートをダブルクリックでプロパティ表示
CakeWalk忘備録
DEXED調査メモ
個人的メモ
DX7のオペレーターのレベル値とレート値の詳細を調べ確認した。VSTiであるDEXEDでも同様の効果が見られた。
docs.google.com
デシベルに関して
音楽で扱われる単位:デシベルは音の強さ、音圧の「レベル」を対数で表したものと言える
基準1からの10000倍の音圧をレベル表現した場合
となる。つまり80dBは物理的に基準からの10000倍の音圧である事がわかる
従ってdBと物理量の関係をグラフで見ると

このような指数曲線のグラフになり人間は、この曲がったグラフを「感覚的に直線的な変化として感じて」いる
95dBなら
となる。DAW等で音声をモニタリングすると20dB~95dBぐらいまでヘッドフォンなどで音楽を視聴していると聴き取ることが出来る
つまり10倍~56000倍の物理的音圧の変化を感じ取れる器官を人類は持っていると考えられる
FM音源で生成される倍音の周波数に関して
キャリア、モジュレーターの音量レベルに応じて倍音は増えていくがDEXEDの場合、キャリアLevel=80、モジュレーターLevel=66で基音の左右に3本程、計7本の倍音が生成される
この倍音はキャリアとモジュレータのレシオの設定、DEXEDの場合「coarse」、VOPMの場合「MUL」によって等差数列の関係で生成される
一般的な等差数列の式は で表されるがFM音源の場合、右側を
、左側を
とした場合
で表せる。の方は絶対値でキャリアの値が低い場合、0倍以下から折り返される倍音を表す(キャリアの値が高い場合、折り返されず左右に広がる)
キャリアのレートが1、モジュレーターのレートが3の場合、、
として
という数列が出来上がる。まとめると「×1、×2、×4、×5、×7、×8、×10」の位置に整数倍音が出来る
以下のスクリーンショットはA3=440Hzを基音とした上記に該当する音色を鳴らした様子で、それぞれの倍音がこの数列通りに出力されている様子が確認できる

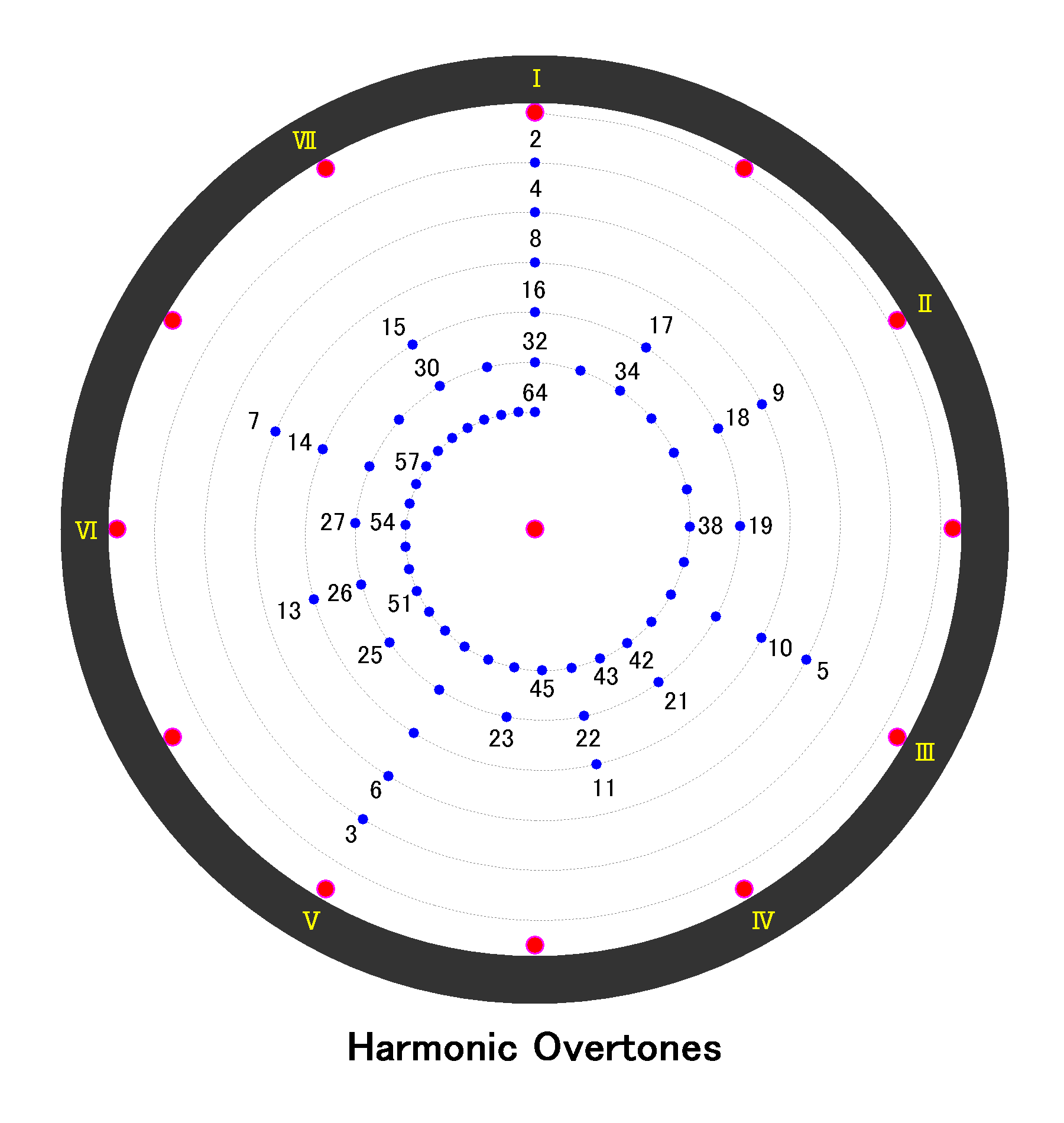
これらの倍音は周波数により音程を持ち基音に対して相対的な関係を持つ。以下wikipediaの倍音の記事(倍音 - Wikipedia)より引用
赤い印が平均律の半音を表している。例えば青丸1をC3にした場合、青丸5はIII周辺なのでE5になり、青丸10はE6になると考える
VOPM追加資料
自分用の忘備録です。
キャリアとモジュレーターのレシオ関係
| carrier:modulator | ||
| 1:1 | ノコギリ波 | 金管楽器、弦楽器、ブラス、ストリングス、ピアノ |
| 1:2 | 低矩形波(近似三角波) | クラリネット、木管楽器、ハープ |
| 1:3 | パルス波 | ピッキング、弦楽器、オーボエ、ダブルリード、木管楽器 |
| 1:4 | 高矩形波 | (矩形波と同上) |
| 1:5 | 基音から離れた位置に倍音のペアが出現 | マリンバ、ヴィブラフォン、チューンドパッカーション |
| 1:6以上 | (同上) | 金属質が出てくる。FM音源特有の音がプラス |
直列で複数並べた場合、キャリアに近い方からモジュレーターが順番に処理されていく。
キャリアに対してY字でモジュレータが複数接続されていた場合、モジュレーターの効果は加算合成される。
ADSR
| キャリア―に対して利用する場合 | AEG(Amplifier Envelope Generator)となる | その音色の音のカタチそのものとなる |
モジュレーターに対して利用する場合はあくまでモジュレーションのレベルを制御する。これは倍音操作が含まれているので単純なPEG(Pitch Envelope Generator)とは異なる
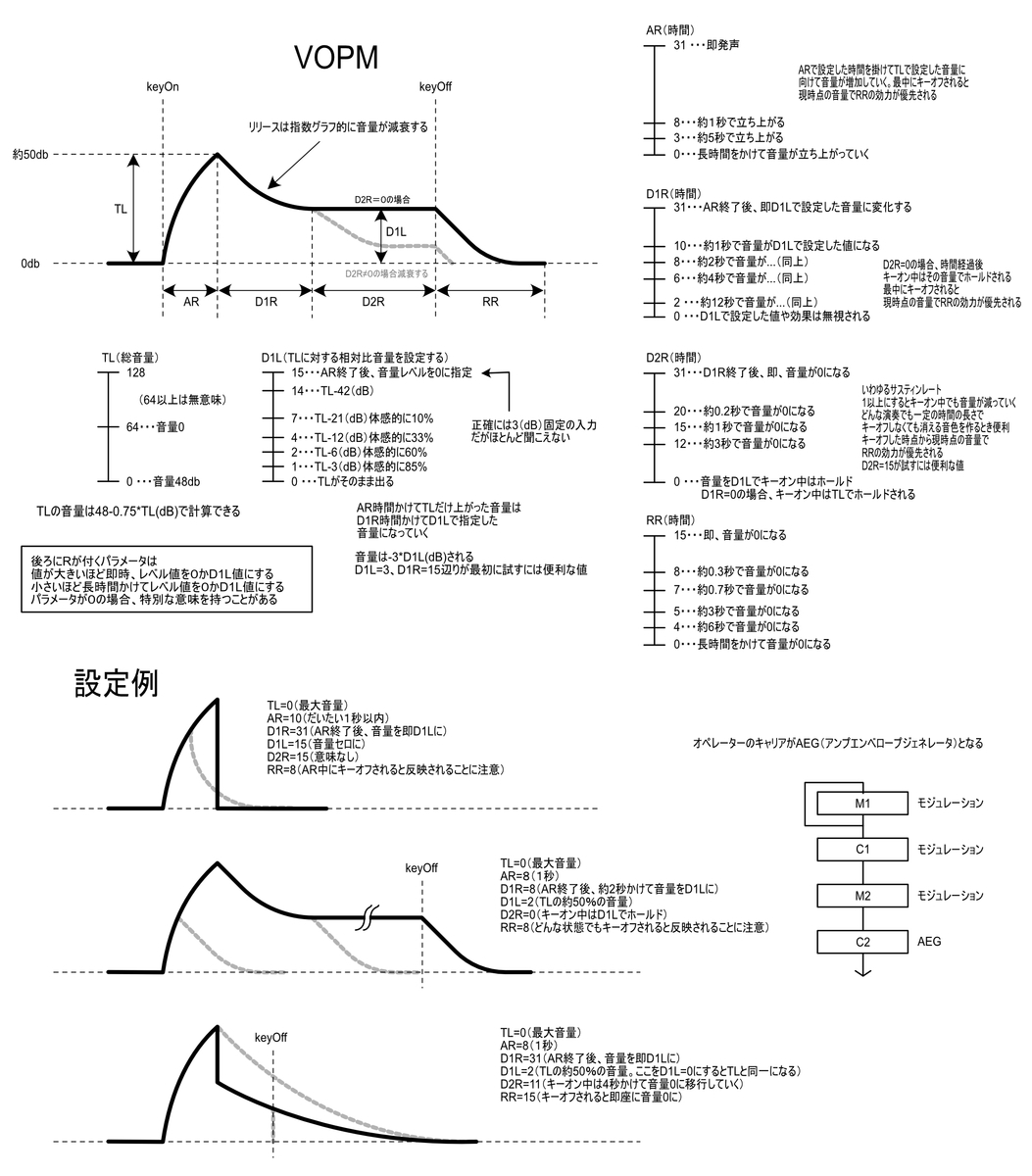
VOPMのMULはMIDIのキーコードの周波数に対して以下で働く
| キーコード周波数倍率 | キーコード例C3 | 周波数例 | |
| MUL=15 | ×30 | b7 | 3924.45 |
| MUL=14 | ×28 | a7+ | 3662.82 |
| MUL=13 | ×26 | g+7 | 3401.19 |
| MUL=12 | ×24 | g7 | 3139.56 |
| MUL=11 | ×22 | f7 | 2877.93 |
| MUL=10 | ×20 | e7 | 2616.3 |
| MUL=09 | ×18 | d7 | 2354.67 |
| MUL=08 | ×16 | c7 | 2093.04 |
| MUL=07 | ×14 | a+6 | 1831.41 |
| MUL=06 | ×12 | g6 | 1569.78 |
| MUL=05 | ×10 | e6 | 1308.15 |
| MUL=04 | ×8 | c6 | 1046.52 |
| MUL=03 | ×6 | g5 | 784.89 |
| MUL=02 | ×4 | c5 | 523.26 |
| MUL=01 | ×2 | c4 | 261.63 |
| MUL=00 | ×1 | c3 | 130.815 |
TX16Wxのオシレーター
TX16Wxのオシレーターを設定しオクターブ4のラ(A)で一周期の波形を記録した
Sine

Triangle

Saw

Integrated Saw

Square

Rect

Half Rectfied Sine

Full Rectfied Sine

Half Rectfied Saw

Triangle Pulse

Trapezoid

Ramp

Stairs

FM音源_忘備録
FM音源の仕組み
VOPM
VOPMなどのFM音源は以下の仕組みを持つ

insideX68kより抜粋。これは各パラメータの動作を分かりやすく図で示したもので何を対象に値が働くか非常にわかりやすい。
ここで重要なのはFM音源の回路内部にSIN波形テーブルがありフェーズジェネレーター(PG)と呼ばれる0から2πまでの数字を出力する
回路があるという部分。このフェイズジェネレーターというのは数学的に式で表すと以下のようになる

ここでのxは時間を表している。いきなりAEG((アンプ)エンベロープジェネレーター)とDT1,DT2(デチューン)を考えると仕組みが分かりづらくなるので
シンプルにそれらの値は1に固定して考えるとキャリアとモジュレーターのふたつのオペレータを合わせて出力した場合の式とグラフは以下のようになる

(以下PocketCasの式)
//inside x68k p263
//FMシンセのあたらしいトリセツ p133参照
AEGalpha:=1
AEGbeta:=1
mul1:=1
mul2:=1
omegaT:=2π*(mul1*x-floor(mul1*x))
phyT:=2π*(mul2*x-floor(mul2*x))
//キャリアとモジュレーターを合わせたFM音源出力波形は以下になる。波形が密集するとピッチは高くなる
Asin:=sin(omegaT+sin(phyT))
//アンプエンベロープジェネレーターまで考えた時の出力
out:=AEGbeta*sin(omegaT+AEGalpha*sin(phyT))


