最小二乗法の学習忘備録 - Unityと数学と音楽の学習帳

該当記事のディテールを補足する個人的な忘備録

以下のサイトを参考に最小二乗法の仕組みを学習する
qiita.com

基本戦略

「基本戦略」の部分をグーグルスプレッドシートで確認したものが以下になる

docs.google.com

最小化する

「極大極小の考え方でいうと、a, bそれぞれに対して、微分して0になるところが最小点になります。」の語句の意味をIOSアプリのPocketCasを利用して再確認すると以下になる

例えば二次関数の微分に対して０になる方程式を解くと以下の様に最小点のx=1.5が算出できる
f:id:cqbosinko:20170713003931p:plain

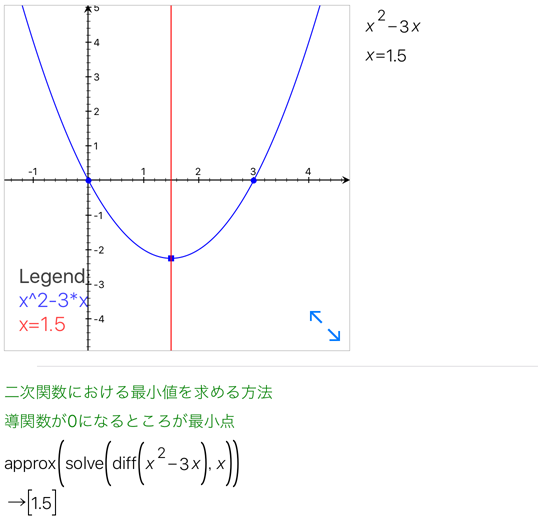
これは他のn次数関数に対しても同様で三次関数の場合、グラフの谷山になるx位置
x=-3.0とx=-1/3が算出できる。つまりグラフの傾きが0になる位置がわかる仕組みを利用する
f:id:cqbosinko:20170713004657p:plain

5次関数で以下のようになる。微分の強力な解析能力が実感できる
f:id:cqbosinko:20170713004901p:plain

この解析能力をaとbの二変数関数である ${ \left( y_{ i }-a{ x }_{ i }-b \right) }^{ 2 }$ に対して利用する為に偏微分しようという訳である。偏微分はaとbに対して行い他の変数は定数と扱われる。導かれた導関数が０になる連立方程式を解くと最小点の位置を通る一次関数の係数が解るという仕組みになる

実際の計算

あてはめる関数式は直線をあらわす一次関数。これを回帰式と呼ぶ

$f\left( x \right) =ax+b$

回帰式と実際に集計した値との誤差を求める式が以下になる
y値、x値はN次のベクトル。これらを総和を利用しながら誤差の総和Jの値を導く
aとbは未知数でJの値を最小にしながら、これらの値を求める事が目的となる

$J\quad =\quad \frac { 1 }{ 2 } \sum _{ i=1 }^{ N }{ { \left\{ y_{ i }-\left( a{ x }_{ i }+b \right) \right\} }^{ 2 } } \quad =\quad \frac { 1 }{ 2 } \sum _{ i=1 }^{ N }{ { \left( y_{ i }-a{ x }_{ i }-b \right) }^{ 2 } }$

シグマの中身は常に二乗されるので値は絶対値、距離、正数となる
従って、この二次関数の微分された関数式は0になる所が最小点に必ずなる（最大値になる可能性は無い。だからこの計算手法は「最小二乗法」と呼ばれる）
関数式の中にaとbの二変数の未知数があるので、それぞれ偏微分して０になる式を導き連立方程式を組む必要がある
偏微分には例題となるブログでは合成関数「 $\left\{ g\left( f\left( x \right) \right) \right\} '=g'\left( f\left( x \right) \right) \cdot f'\left( x \right)$ 」を利用している

$\frac { \partial J }{ \partial a } \quad =\quad \frac { 1 }{ 2 } \sum _{ i=1 }^{ N }{ 2{ \left( y_{ i }-a{ x }_{ i }-b \right) } } \left( { -x }_{ i } \right) \quad =\quad a\sum _{ i=1 }^{ N }{ { x }_{ i }^{ 2 } } +b\sum _{ i=1 }^{ N }{ { x }_{ i } } -\sum _{ i=1 }^{ N }{ { x }_{ i }y_{ i } } \\ \frac { \partial J }{ \partial b } \quad =\quad \frac { 1 }{ 2 } \sum _{ i=1 }^{ N }{ 2{ \left( y_{ i }-a{ x }_{ i }-b \right) } } \left( -1 \right) \quad =\quad a\sum _{ i=1 }^{ N }{ { x }_{ i } } +b\sum _{ i=1 }^{ N }{ 1 } -\sum _{ i=1 }^{ N }{ y_{ i } }$

最終的な回帰式は行列計算の形になる
これは連立方程式を計算機で解く為で、機械を使って問題を解く適切な形となっている

$\begin{cases} a\sum _{ i=1 }^{ N }{ { x }_{ i }^{ 2 } } +b\sum _{ i=1 }^{ N }{ { x }_{ i } } -\sum _{ i=1 }^{ N }{ { x }_{ i }y_{ i } } =0\quad \Leftrightarrow \quad a\sum _{ i=1 }^{ N }{ { x }_{ i }^{ 2 } } +b\sum _{ i=1 }^{ N }{ { x }_{ i } } =\sum _{ i=1 }^{ N }{ { x }_{ i }y_{ i } } \\ a\sum _{ i=1 }^{ N }{ { x }_{ i } } +b\sum _{ i=1 }^{ N }{ 1 } -\sum _{ i=1 }^{ N }{ y_{ i } } =0\quad \Leftrightarrow \quad a\sum _{ i=1 }^{ N }{ { x }_{ i } } +b\sum _{ i=1 }^{ N }{ 1 } =\sum _{ i=1 }^{ N }{ y_{ i } } \end{cases}\\ \\ \begin{pmatrix} \sum _{ i=1 }^{ N }{ { x }_{ i }^{ 2 } } & \sum _{ i=1 }^{ N }{ { x }_{ i } } \\ \sum _{ i=1 }^{ N }{ { x }_{ i } } & \sum _{ i=1 }^{ N }{ 1 } \end{pmatrix}\begin{pmatrix} a \\ b \end{pmatrix}=\begin{pmatrix} \sum _{ i=1 }^{ N }{ { x }_{ i }y_{ i } } \\ \sum _{ i=1 }^{ N }{ y_{ i } } \end{pmatrix}\quad \quad \Leftrightarrow \quad \begin{pmatrix} a \\ b \end{pmatrix}={ \begin{pmatrix} \sum _{ i=1 }^{ N }{ { x }_{ i }^{ 2 } } & \sum _{ i=1 }^{ N }{ { x }_{ i } } \\ \sum _{ i=1 }^{ N }{ { x }_{ i } } & \sum _{ i=1 }^{ N }{ 1 } \end{pmatrix} }^{ -1 }\begin{pmatrix} \sum _{ i=1 }^{ N }{ { x }_{ i }y_{ i } } \\ \sum _{ i=1 }^{ N }{ y_{ i } } \end{pmatrix}$

この行列式に実測値をあてはめ計算していく

${ x }_{ i }=\left\{ 4,15,30,50 \right\} \\ y_{ i }=\left\{ -17,-4,-7,25 \right\}$

$a\sum _{ i=1 }^{ N }{ { x }_{ i }^{ 2 } } \quad =\quad a\left( { 4 }^{ 2 }+{ 15 }^{ 2 }+30^{ 2 }+{ 50 }^{ 2 } \right) \quad =\quad 3641a\\ b\sum _{ i=1 }^{ N }{ { x }_{ i } } \quad =\quad b\left( 4+15+30+50 \right) \quad =\quad 99b\\ \sum _{ i=1 }^{ N }{ { x }_{ i }y_{ i } } \quad =\quad 4\times -17+15\times -4+30\times -7+50\times 25\quad =\quad 912\\ a\sum _{ i=1 }^{ N }{ { x }_{ i } } \quad =\quad a\left( 4+15+30+50 \right) \quad =\quad 99a\\ b\sum _{ i=1 }^{ N }{ 1 } \quad =\quad 4b\\ \sum _{ i=1 }^{ N }{ y_{ i } } \quad =\quad -17+-4+-7+25\quad =\quad -3$